PoolTogether V5 Protocol Design

PoolTogether V5 is the newest version of the prize savings protocol; where yield on deposits is awarded as random prizes to depositors. This version is designed to be a hyperstructure; an autonomous, immutable protocol that can be permissionlessly extended by anyone.

Overview

A prize savings protocol gives users a chance at a large upside without risking their deposit. Each day, the yield from deposits is awarded randomly as prizes. Users have a chance to win everyone else's yield!

What's New in V5

This version of the protocol brings some major improvements:

• Users can swap or zap into prize tokens; there is no need to "activate" your tokens. This enables distribution through AMMs and other swap interfaces.
• Users automatically receive their prizes. No claim needed! The tokens will be transferred to their wallets.
• Supports multiple tokens, and all tokens share one big pool of prizes so that prizes are as large as possible!

The Hyperstructure

This version is also our first "hyperstructure", in that:

• The core protocol is fully autonomous. There is no administrator or parameters than can be adjusted.
• The core protocol is immutable; no code can be changed.
• Anyone can add new tokens or yield sources to the protocol; it can be extended permissionlessly
• All "maintenance" functions can be triggered by anyone and are incentivized

In this way, anyone can build on the protocol and know that it will never change and cannot be stopped. It becomes a solid foundation on which prize savings can be built.

Deployments

PoolTogether V5 will be deployed on a variety of EVM-compatible networks. Each deployment will include the core contracts and a set of factories that allow anyone to easily extend the protocol with new tokens or yield sources.

The core contract is the Prize Pool; this is the contract that holds prize liquidity and disburses prizes. Each chain will be an island of prize liquidity; prizes won't be shared across chains.

Flow of Funds

Let's take a closer look at how funds would flow through a V5 deployment. Below is a simplified diagram:

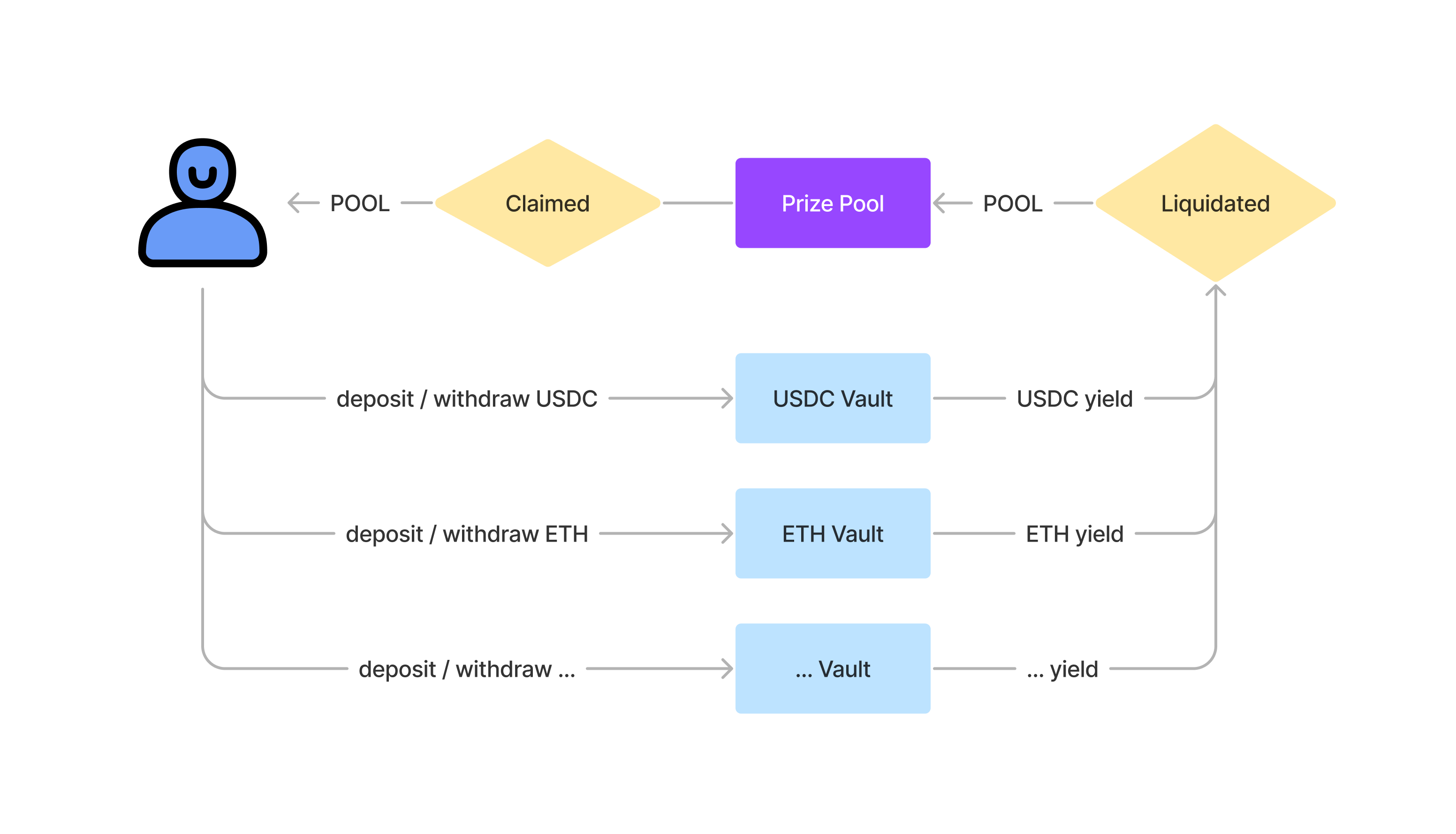
The diagram above shows the POOL token as the prize token, but this will vary across deployments. The latest deployment on Optimism uses WETH as the prize token.

Step-by-step

1. Users deposit tokens into Prize Vaults.
2. Prize Vault yield is liquidated for the prize token and sent to the Prize Pool contract.
3. Prizes are claimed and sent to the user

We can see that there are three main stages in the process: deposit, liquidation, and prize distribution.

Deposits

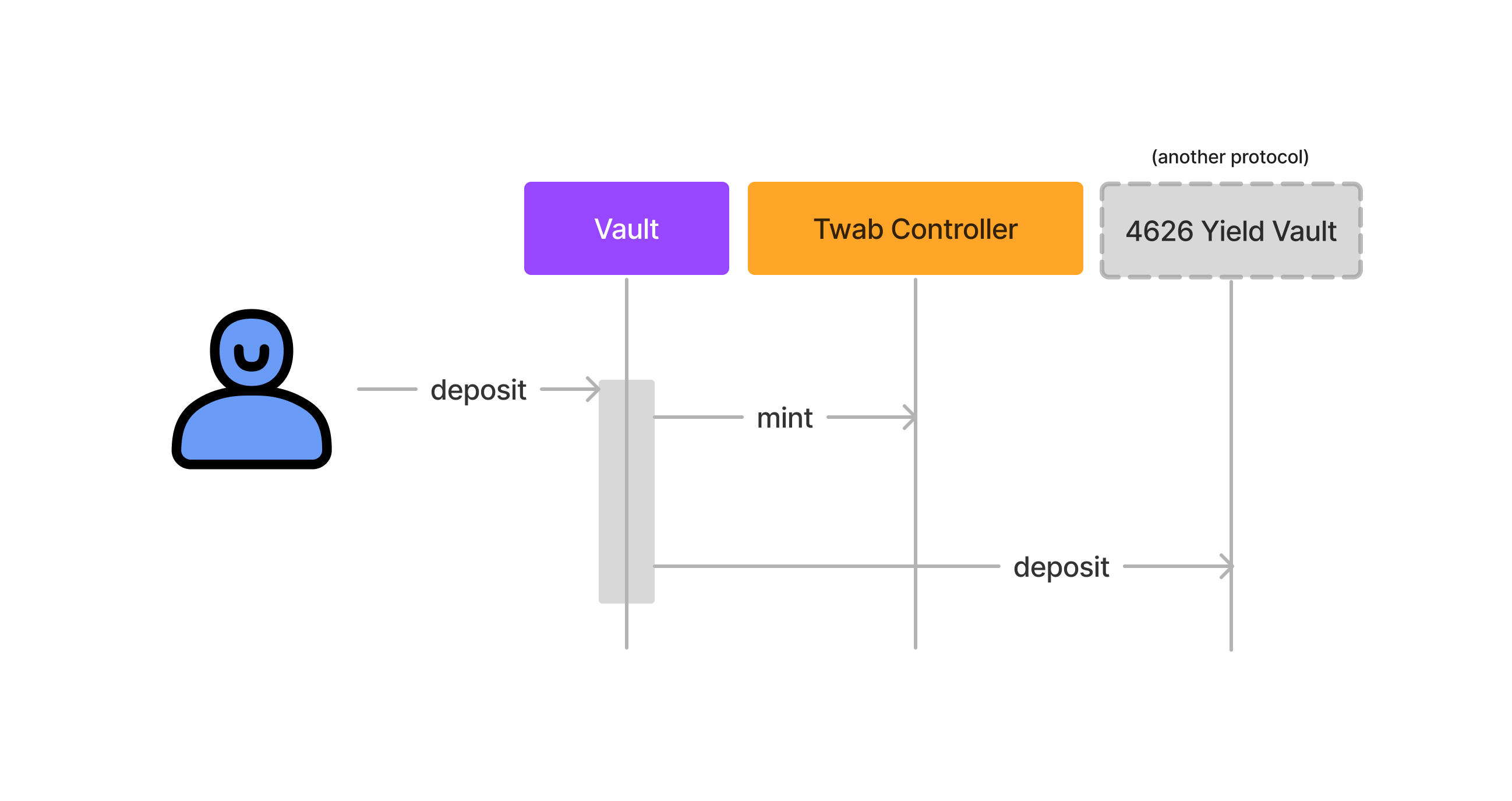
When users "deposit into PoolTogether" they are really depositing into an ERC4626 vault that contributes its yield to the Prize Pool and tracks deposits using the Twab Controller.

The vault can be created by anyone; and PoolTogether V5 has a Prize Vault Factory that makes deploying new vaults a snap. The default factory vault is an ERC4626 Vault that uses another ERC4626 vault to generate yield. When a user creates a new vault they must pass the address of the ERC4626 yield vault. A Prize Pool can support any number of vaults.

In order for users to be eligible to win prizes, their balances must be tracked in the Twab Controller. The default PoolTogether prize vault doesn't actually store any balances internally; all balances are stored in the Twab Controller.

Yield accrued by the underlying 4626 vault is exposed to an external liquidator, which liquidates the yield and contributes the resulting prize token to the Prize Pool.

Interaction Diagram for a Deposit

The Twab Controller

The Twab Controller tracks a users historic balance, so that the protocol can determine how much liquidity they held between two timestamps. There is one controller per deployment. The "Twab" in the name stands for time-weighted average balance, which is the algorithm used to track balances. Any contract may use the Twab Controller to track balances.

The Twab Controller is really tracking two balances: the "owned" balance for a user and the "delegated" balance for a user:

• The "owned" balance is like their token balance; it's the amount of tokens that the user actually controls.
• The "delegated" balance is the total balance that has been delegated to the user. By default users delegate to themselves, but it may also include any balances that have been delegated to them by others.

Historic balance tracking is based on the delegate balance for the user. When querying getBalanceAt or getTwabBetween it will return the balance that had been delegated to them.

Time-Weighted Average Balance

The Twab allows one to calculate the average balance that a user held between two timestamps. Whenever a user's delegate balance changes, the Twab Controller adds a new Twab "observation" to the ring buffer of observations for that user.

A twab observation includes:

• Timestamp: the current timestamp
• Balance: the current delegate balance
• Cumulative Balance: the cumulative twab

The cumulative balance is calculated using the formula:

$cumulativeBalance = lastCumulativeBalance + lastBalance * (timestamp - lastTimestamp)$

Then we can compute the average balance held between observations by computing:

$averageBalance = {(endCumulativeBalance - startCumulativeBalance) \over (endTimestamp - startTimestamp)}$

Liquidation

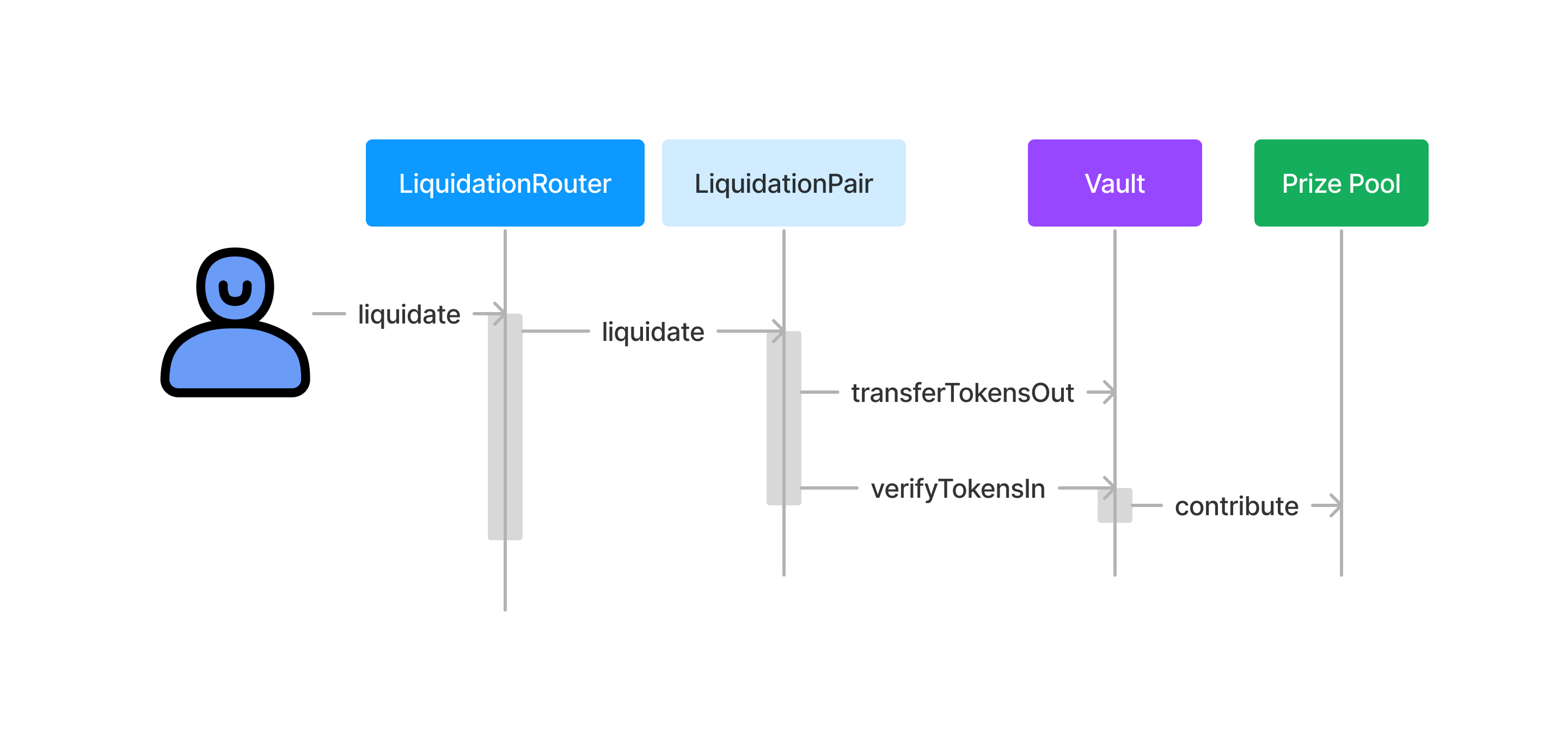
Yield from all the vaults is liquidated for the prize token and contributed to the Prize Pool. This allows chance to be distributed proportionally to all vaults, and for there to be a single deep pool of prize liquidity. No oracles needed.

Each Vault has a corresponding Liquidation Pair that auctions yield for the prize token. Users interact with the Liquidation Pair in order to liquidate vault yield. The pair is responsible for pricing the yield and does so using a Target Period Dutch Auction (TPDA).

Externally-Owned Accounts should interact with the Liquidation Router, as it provides additional checks that ensure the swap occurs correctly.

Iteraction Diagram for a Liquidation

Target Period Dutch Auction (TPDA)

The TPDA is an auction algorithm that prices available tokens based on the last sale price and lowers the price from infinity to zero over time such that the price reaches the last sale price at the end of the specified target period.

The TPDA liquidators can be configured to target 'x' number of liquidations per day to fit the needs of the prize vault. In addition, a "smoothing" parameter can be applied such that the liquidator will only auction a set percent of the available yield each time. This simple mechanism allows the auctions to handle yield that fluctuates significantly by setting the smoothing percentage to a higher value.

Contributing to Prize Pool

When yield is liquidated, the prize token is transferred to the Prize Pool and the Vault tells the Prize Pool that it contributed. The Prize Pool recognizes the balance increase, and updates that vault's contribution.

Prize Distribution

The Prize Pool releases prizes in periodic Draws. Each Draw is allocated a portion of the prize liquidity, and the prize structure is determined by the number of prize claims from the previous draw. Prize claims for a Draw begin after the completion of a random number generation auction. Prize claims are incentivized by variable-rate gradual dutch auction so that users don't need to claim for themselves.

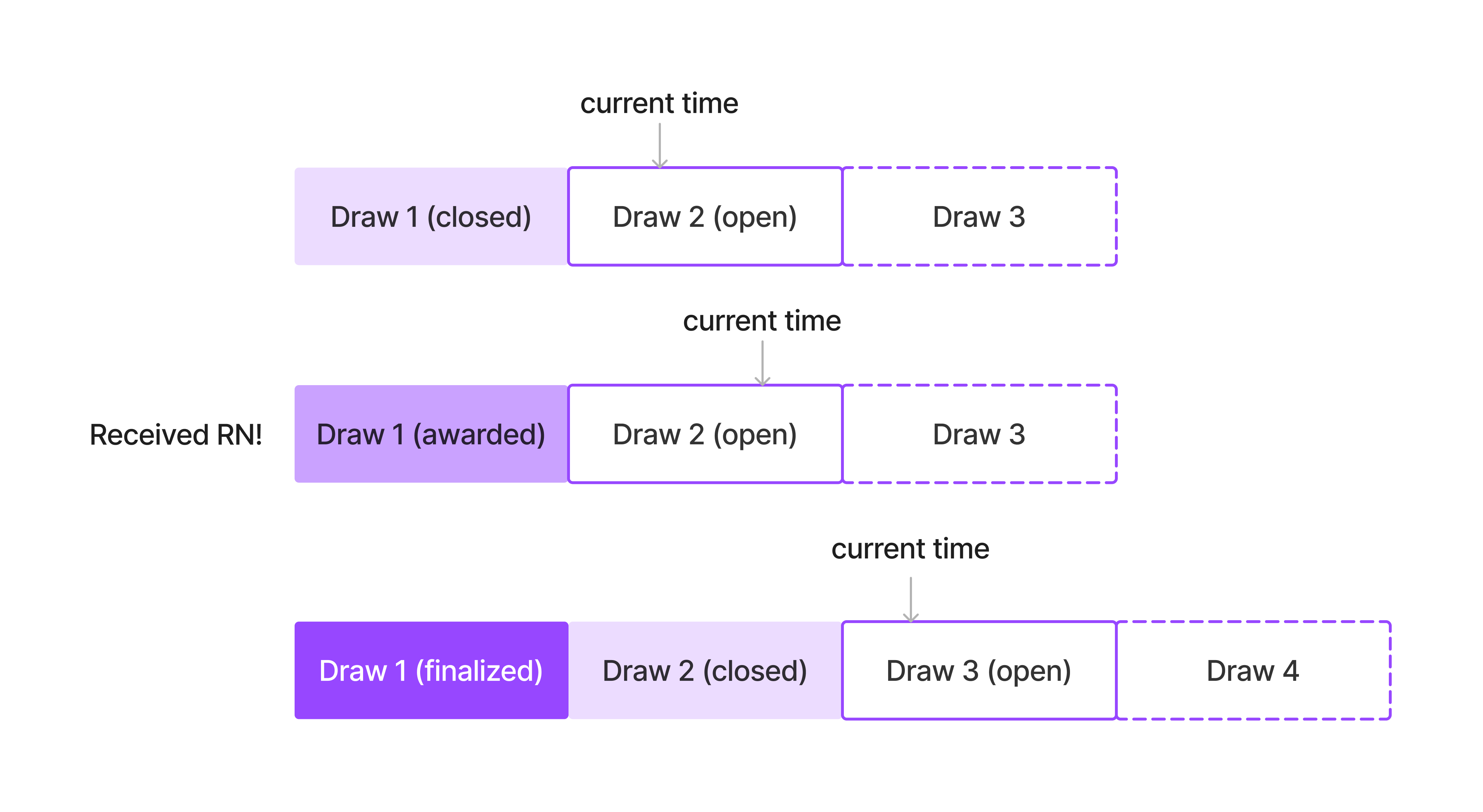
Draws

Draws are like a numbered timeframe; the Prize Pool is initialized with a draw period in seconds, and the first draw start time. Draw 1 is the first period of time, Draw 2 is the second period of time, etc. Each Draw goes through a lifecycle of states:

• Open: the open draw is the one that is currently receiving contributions from vaults. It is the next draw to close.
• Closed: once the draw end has elapsed, the draw is considered closed. It will no longer receive new contributions.
• Awarded: when the random number is submitted, the most recent closed draw becomes awarded and prizes can be claimed.
• Finalized: draws become finalized after one draw period has elapsed after they close. After this time no prizes can be claimed.

Prize Structure

Each draw is allocated the accrued liquidity from the contributions during the draw period, as well as any leftover liquidity from previous draws. This liquidity is then distributed across a number of prize tiers and a reserve. Each prize tier has a different prize count and odds of occurring. The reserve is used to fund the RNG auction and backstop prize claims in the event a prize tier runs out of liquidity. When a draw is awarded it computes the number of prize tiers based on the number of claims for the previous awarded draw.

Prize Liquidity

Prize liquidity is distributed into prize tiers and the reserve.

The amount of liquidity that is allocated to a tier per draw is determined by the Prize Pool's configured number of tier shares and reserve shares. If the number of tiers is $n$ then the portion of liquidity allocated to a tier is:

$liquidity = { tierShares \over tierShares*(n-2) + canaryShares*2 + reserveShares}$

The last two tiers are always canary tiers, which have reduced liquidity and special properties.

Canary Tiers

The canary tiers are the last two prize tiers each draw. They are expected to have reduced liquidity compared to normal prize tiers and are not usually distributed to the winners because of their insignificant value (this behavior is configured by the claimer and each vault can use a different claimer).

The first canary tier is expected to be claimed every draw, if it isn't then the next draw will have one less tier than before. Inversely, the second canary tier has slightly smaller prizes and is not expected to be claimed. If it is claimed, then the next draw will have one more tier. This behavior lets current gas prices and incoming yield determine the prize size and prize count.

Prize Counts and Odds

Each prize tier has a different prize count and odds of occurring. This enables liquidity to build up for prizes and to provide a spectrum of sizes and odds.

The prize count is computed based on the tier $t$:

$tierPrizeCount = 4^t$

You can see how tier 0 is the grand prize, as it is the whole tier's liquidity. The highest tier has the highest number of prizes.

The tier odds are also tuned, such that the highest tier has a 100% chance of occurring every draw and the lowest tier (tier 0) occurs every $g$ draws. We call $g$ the grand prize period.

The formula is:

$odds(t) = e^{\frac{\left(\left(t-n+1\right)\cdot\ln\left(\frac{1}{g}\right)\right)}{1-n}}$

Where $n$ is the number of tiers.

The combination of the count and odds results in a broad spectrum of large infrequent prizes and lots of small frequent prizes. Below is a visualization of the prize size over time for a simulation with 4 tiers:

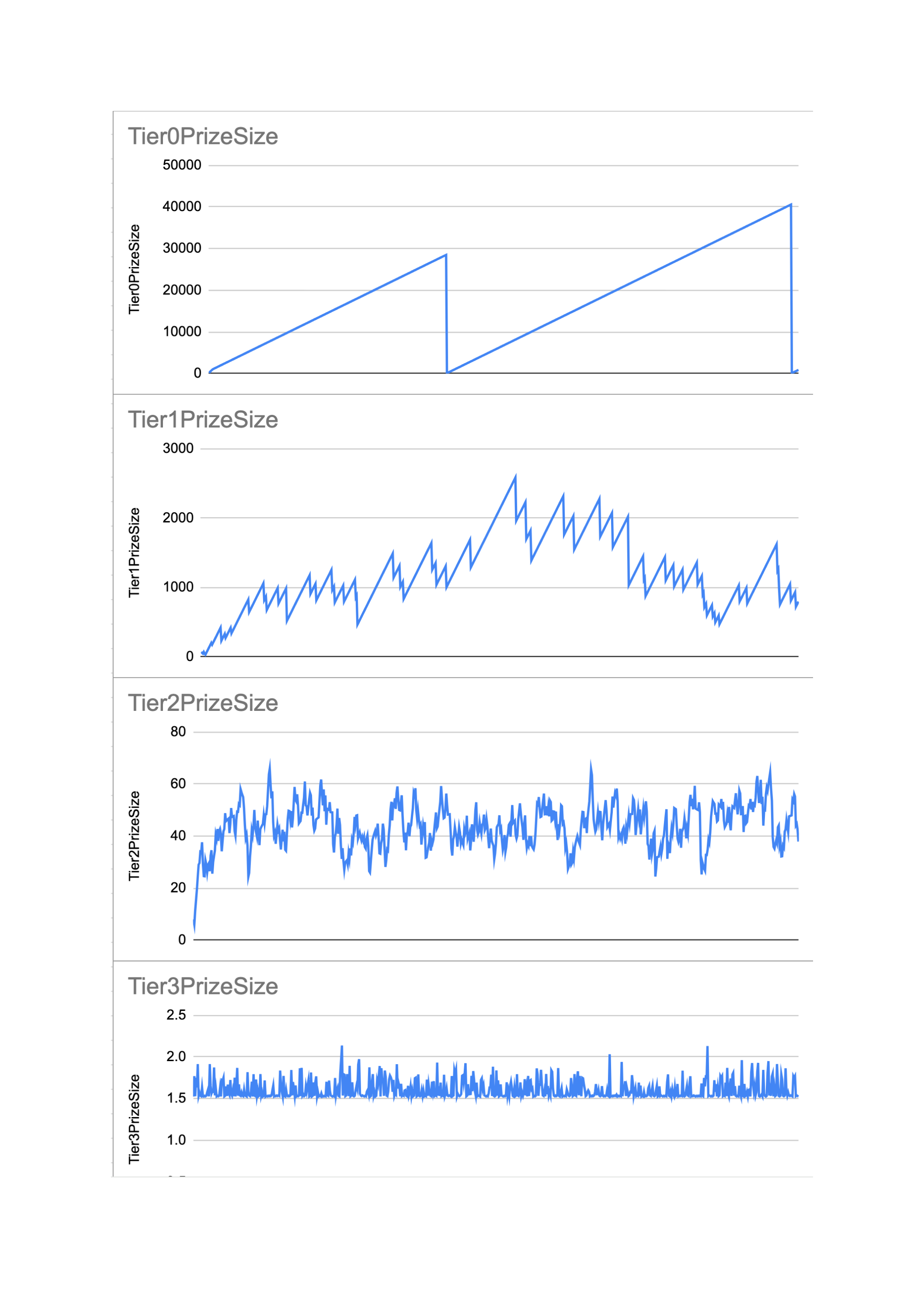
You can see how the highest tier has many small, frequent prizes. While the grand prize builds up to become large and is awarded less frequently.

Adaptive Prize Count

When a draw is awarded, it adjusts the number of prize tiers based on how many prizes were claimed for the previous awarded draw.

We do this quite simply: by using a lookup table of estimated prize counts. When the Prize Pool is constructed it is configured with the grand prize period. The number of tiers must be 4 or greater, and less than or equal to 11. This means we just need to compute the estimated counts for the 8 unique number of tiers.

To compute the number of tiers, we lookup the number of tiers given the last prize claim count and compare it to the estimated count for the number of tiers. Any Unused liquidity in the canary tiers are recycled back into prizes.

RNG Auction

The Prize Pool sources the random number for the awarded draw from a permanently coupled RNG source via a sequence of auctions. These auctions are paid out from the reserve that has accrued in the Prize Pool.

Each time a Draw is to be awarded, two auctions must be completed in sequence:

1. Start RNG: this is the auction to incentivize the RNG request. Some RNG sources, such as Witnet and Chainlink VRF, charge per use.
2. Finish RNG: this is the auction that incentivizes the awarding of the draw after the random number has successfully been generated.

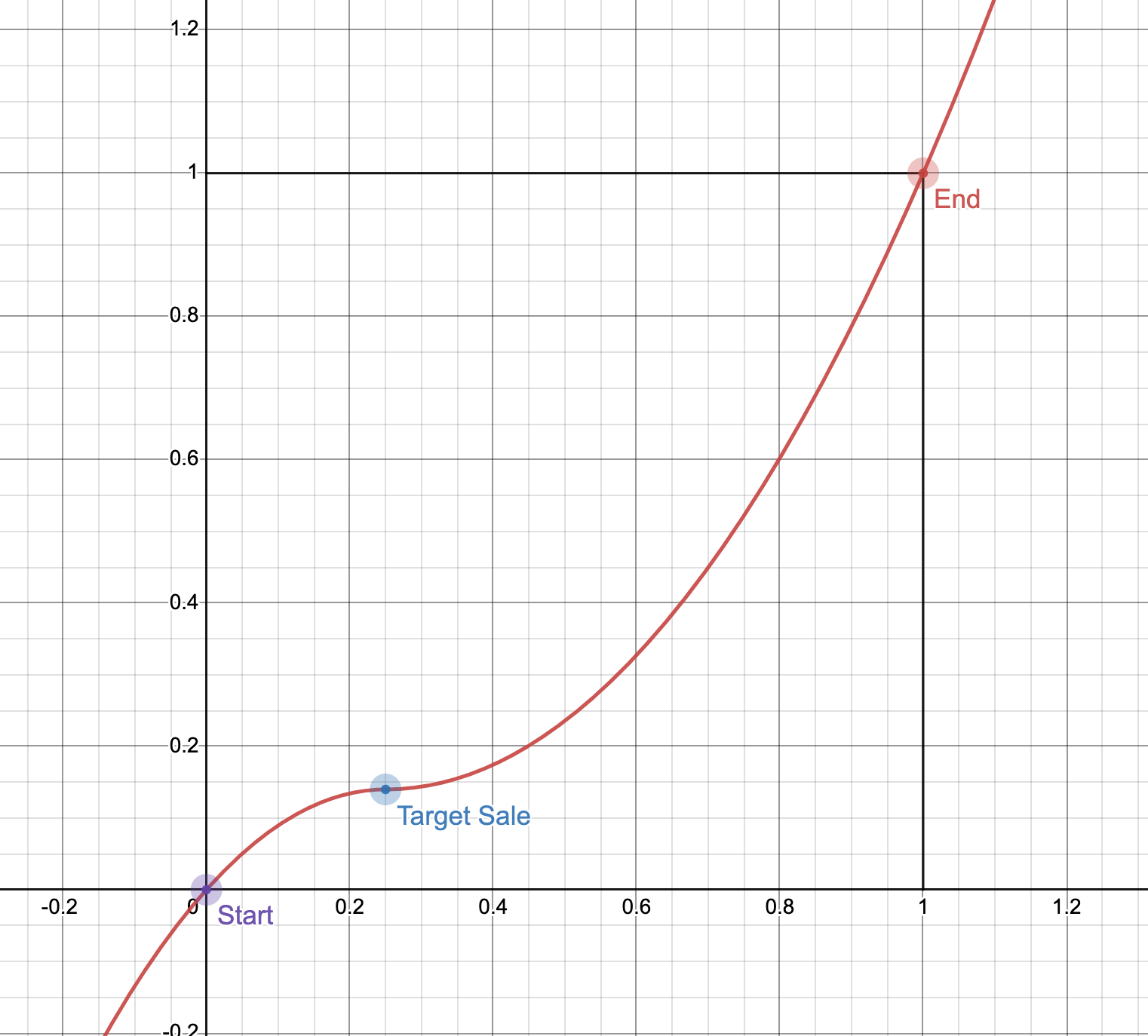
To encourage rapid and consistent price discovery, we use a Parabolic Fractional Dutch Auction. This auction has two phases, both of fixed length of time.

1. The first phase is an inverted parabola, and it's origin places it at the last auction price.
2. The second phase is a parabola whose origin begins at the last auction price, and finishes at 1 at the end of the auction.

In this way, the system will rapidly settle to the previous auction prices and remain near that price for a prolonged amount of time to promote accurate price discovery.

Parabolic Fractional Dutch Auction

Timeline

The auctions have an expiry period which, combined, is half of the draw period. This means that the draw must be awarded within the first half of the next open draw, otherwise it won't be awarded at all. This puts a lower limit on the remaining time to claim prizes during a draw.

Claiming Prizes

After a draw has been awarded prizes can be claimed. Prizes can be claimed until the next Draw closes. Vaults claim on behalf of their users, which gives Vaults flexibility in how they want to handle prizes. The default PoolTogether Vault has a separate "Claimer" contract through which users claim prizes for others. Users (or bots) call the claimer, which calls the Vault, which calls the Prize Pool.

Interaction Diagram for Prize Claiming

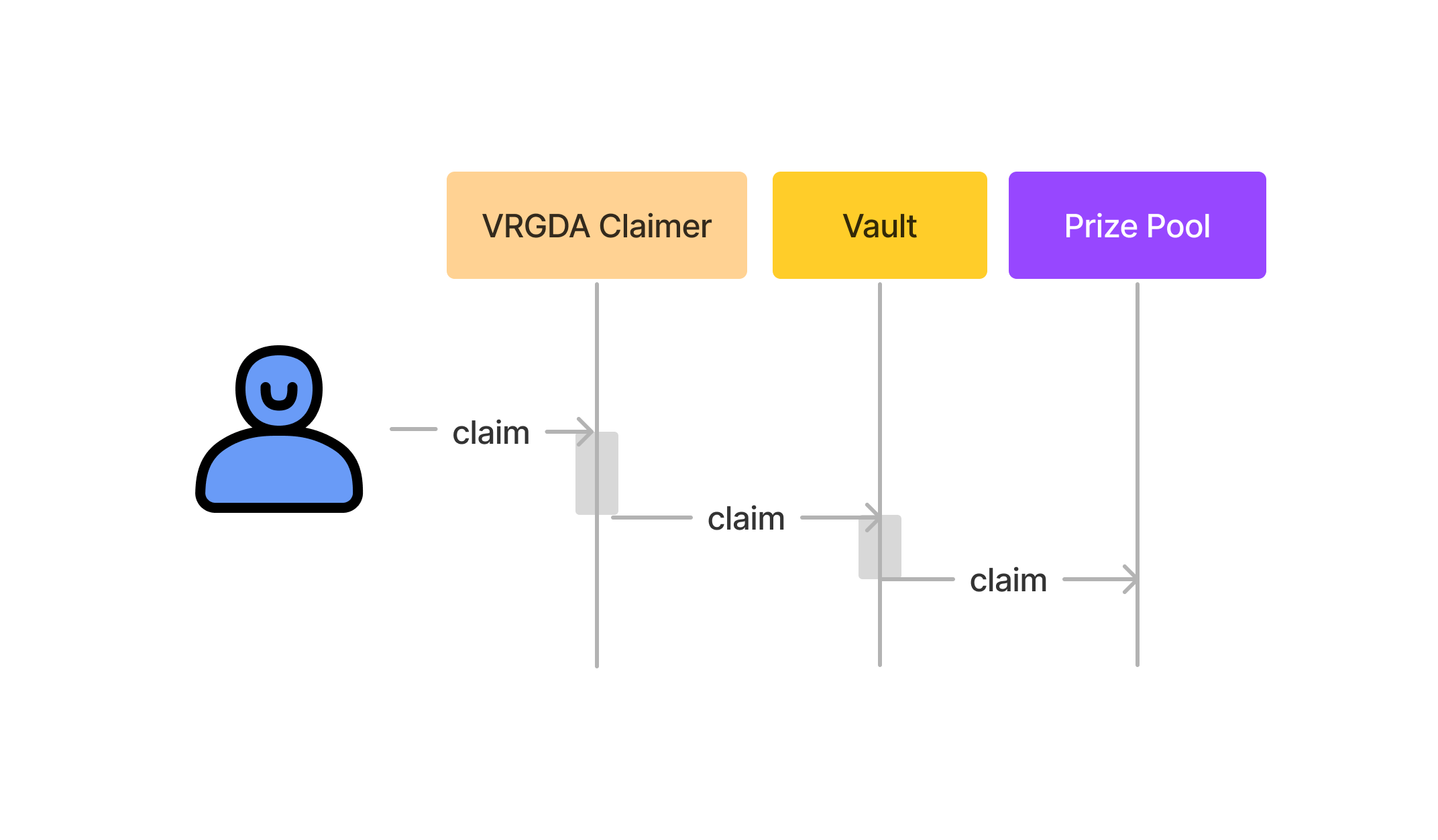
VRGDA Claimer

Once a draw is awarded, the last auction begins: the auction for prize claims. A variable-rate gradual dutch auction is used to reward anyone who claims a prize on a winner's behalf. The reward is taken from the prize itself. The Prize Pool allows Vaults to claim prizes on behalf of their users, so the claim behaviour can be customized by the vault. PoolTogether V5 provides a default VRGDA Claimer that can be plugged into a prize vault with no extra setup or maintenance required.

A VRGDA is a generalization of the continuous dutch auction, in that it raises prices when sales are ahead of schedule and lowers prices when sales are behind schedule.

For PoolTogether V5 we are using the VRGDA as a reverse dutch auction to claim prizes, so it lowers fees when claims are ahead of schedule and raises fees when claims are behind schedule. This allows us to ensure that all prizes are claimed before the next draw is awarded, at which point the prizes can no longer be claimed.

The "schedule" of claims is based on a count and time frame. Recall the estimated claim count from the adaptive number of tiers? We use that same number to compute the schedule. The schedule starts immediately after the draw is awarded, and is set to take one quarter of the draw period. This provides plenty of leeway in the event that there are more prizes, statistically, for a given draw. It's highly unlikely that a draw will see a variance of double the expected prizes, so we believe a quarter of the draw period is sufficient.

Winner Eligiblity

The Prize Pool determines whether a user has won a prize by checking if a pseudo-random number is within a certain range. The PRN is generated such that it is unique per draw, tier, vault and user. The number range is used to tune the odds based on the prize frequency and the user's eligibility.

There are three steps we take:

1. Calculate the pseudo-random number
2. Calculate the winning zone
3. Check if the PRN is less than the winning zone

Pseudo-Random Number

First we calculate a pseudo-random number is a keccak256 hash of the abi-encoded params:

uint256 pseudoRandomNumber = uint256(keccak256(abi.encode(drawId, vault, user, tier, prizeIndex, drawRandomNumber)))

We include the following params to ensure the PRN is unique:

• drawId: the id for the awarded Draw
• vault: the address of the vault that is claiming the prize
• user: the address that won the prize
• tier: the prize tier that was won
• prizeIndex: the prize index within the tier that was won. E.g. if a tier 2 has $4^2$ prizes, then prize indices between 0 and 15 (inclusive) can be submitted.
• drawRandomNumber: the Draw's random number

Winning Zone

Next we calculate the winning zone. The winning zone is a multiple of three fractions: the user's time-weighted average balance, the tier odds, and the vault portion:

uint256 winningZone = tierOdds * userTwab * vaultPortion

• The tier odds is a function that determines the prize tier frequency
• The user's time-weighted average balance is the average balance they held for the duration of the prize tier accrual.
• The vault portion is the fraction of prize liquidity that was contributed by the vault for the duration of prize tier accrual.

The tier odds function creates a spectrum of prize frequencies between the yearly grand prize and the daily prizes. For more details see the Prize Pool.

The prize tier accrual duration is computed based on the tier odds. Essentially it's time periods based on the prize frequency function above; which means that accrual durations will range between one GP period and a single draw.

The user's time-weighted average balance is measured between the timestamps drawClosedAt - duration and drawClosedAt. E.g. for the yearly grand prize it will be their average balance for the preceding year, and for the daily prize it will be their balance for the preceding day.

The vault portion is the portion of prize liquidity that was contributed by the vault. It is also measured between two timestamps:

vaultPortion = vaultContributedPrizeLiquidityBetween(drawClosedAt - duration, drawClosedAt) / totalContributePrizeLiquidityBetween(drawClosedAt - duration, drawClosedAt)

Check if PRN is in the Winning Zone

Now that we have our PRN and Winning Zone, we can determine whether the user won a prize from a certain tier.

We first squeeze the PRN into a smaller PRN within the vault's total average supply for the prize tier accrual duration. Then, we check to see if that number is less than the winning zone.

bool userWon = PRN % vaultTotalAverageSupply(drawClosedAt - duration, drawClosedAt) < winningZone

Note that the above is simplified; we use a custom modulo function that handles modulo bias.

Claim Your Prize!

When a prize claim is submitted successfully, the Prize Pool transfers tokens to the winner and increases the claim rewards for the claimer (if any).